Correctness of Codes using Deep Learning Platforms

This project ensures the correctness of deep learning training and inference codes built on top of TensorFlow/PyTorch.

Deep learning models have made remarkable advancements in solving complex and diverse problems. The training and inference of these models are coded built on platforms like TensorFlow and PyTorch. This coding requires a programming paradigm that differs significantly from traditional ones. For instance, programming logic relies more heavily on intensive matrix operations and activation functions than traditional programming structures such as branches and loops. As a result, new defects have emerged in deep learning code, and we need to rethink the problem of verifying code correctness and providing provably correct fixes to these defects.

In my research on providing provable guarantees for the correctness of deep learning code, I pose the following questions: What are these new defects? Which defect type is of most concern to the deep learning community? The first question led me to conduct a pioneering empirical study of novel defects in deep learning code. This study found that numerical defects, which often manifest as NaN or INF during neural network computations, are prevalent in deep learning code and can significantly impair the model accuracy, potentially leading to system crashes. This finding addressed the second question and guided my work on ensuring deep learning code is free of numerical defects.

Papers: An empirical study (ISSTA2018), DEBAR (FSE2020), RANUM (ICSE2023)

Key ideas:

1. A pioneering empirical study of defects in deep learning code.
2. An abstract interpretation technique for verifying the absence of numerical defects.
3. A framework for reliability assurance against numerical defects by providing failure-exhibiting tests and provably correct fix suggestions.

A pioneering empirical study Motivated by the need to investigate emerging defects in deep learning code, I conducted a pioneering empirical study on the root causes, symptoms, and fixing strategies of these new defects. This empirical study not only serves as a bedrock of my work but also inspires numerous initiatives in the research community. For example, our study identified new defects such as unaligned-shape defects, where the shape of a tensor, a data structure predominantly used in deep learning, does not align with its expected shape. Subsequently, a corresponding approach has been proposed to detect this new defect. Additionally, Islam et al. conducted a further empirical study and “adapted the classification scheme of root causes and bug effects” from our study.

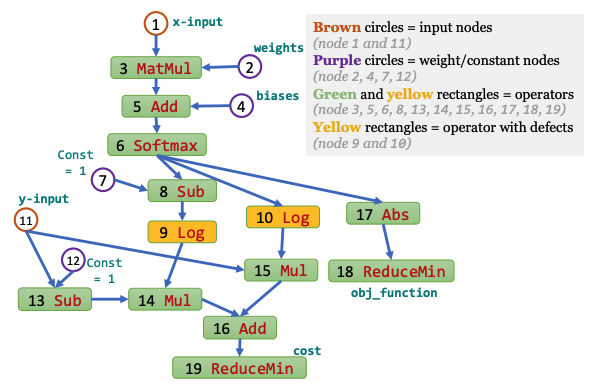
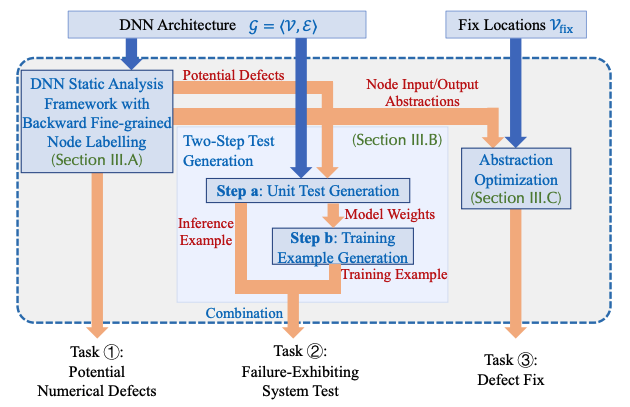
Verification of the absence of numerical defects My work, DEBAR, detects numerical defects in deep learning code. It can either construct a proof confirming the absence of numerical defects within the code or identify suspicious computational graph nodes that may have numerical defects. To construct such proof, I design refined yet scalable abstract domains, tensor partitioning and interval with affine equality relation, to over-approximate the output range of each node in the computational graph. If a node receives an invalid range or its output overflows, DEBAR will report this node as suspicious. And if no such node exists in the code, DEBAR then gets a correctness proof owing to the soundness of abstract interpretation. DEBAR is highly scalable as it only takes an average of 12.1 seconds for each model, while maintaining a low false positive rate of 7.7%. DEBAR has received recognition with the ACM SIGSOFT Distinguished Paper Award at FSE 2020 and it detected 11 real-world bugs of 48 models implemented in an official repository maintained by the TensorFlow team (See, e.g., defect 1, defect 2).

Provably correct fixes to numerical defects Once the defects are identified, developers need to fix them. We found that developers either provided no fixes or designed heuristic fixes that did not eliminate these defects, such as reducing the learning rate. Such heuristic fixes often delay the triggering of numerical defects during training and further obscure the defects. Our work, RANUM, automatically synthesizes provably correct fixes to these defects for developers. The fixes take the form of clipping the input ranges of some computational graph nodes. Striking the right balance with these input ranges is critical; overly tight ranges can hinder the model accuracy, whereas overly wide ranges may still result in numerical defects. We propose an abstraction optimization algorithm to find the tightest input ranges that provably eliminate the defects.